Ya sabemos que las redes sociales las carga el diablo, y en concreto Twitter nos puede servir para aprender muchas cosas interesantes y compartir papers, pero también para montarnos discusiones eternas basándonos en cualquier tontería que se nos ocurra. Hoy os voy a hablar de uno de esos temas recurrentes que asoman de vez en cuando en esta red social, generando montones de hilos y debates y peleas… que al cabo de un tiempo se olvidan y vuelven a repetirse. Como las estaciones o como algo inevitable. En este caso, el debate es en torno a la estadística, y por eso nos interesa.

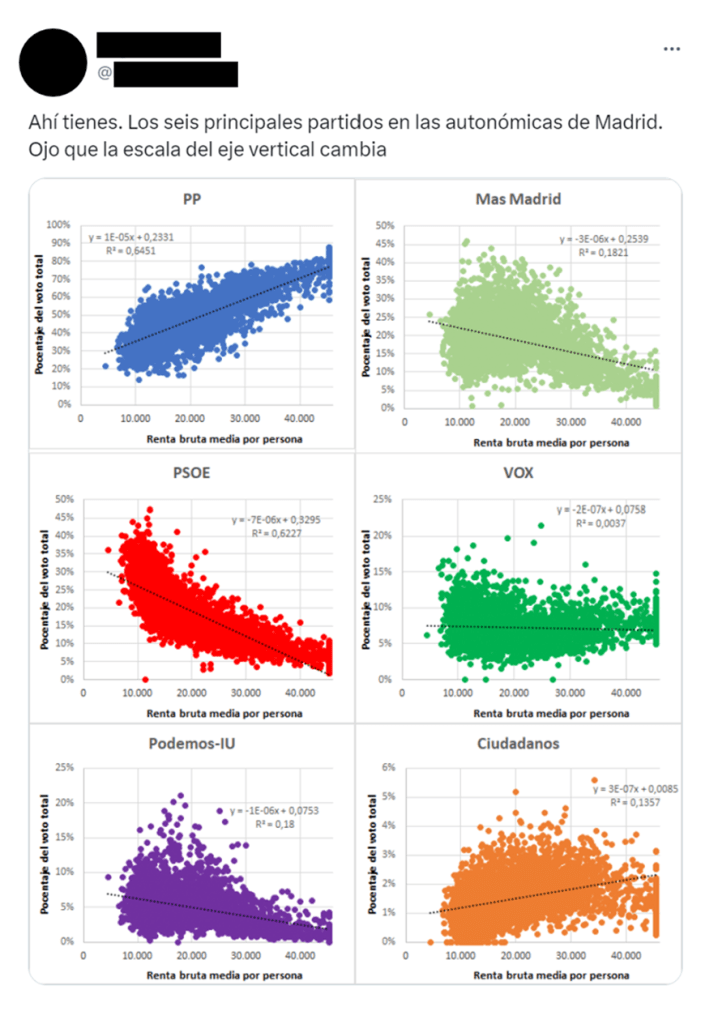
Generalmente, todo empieza cuando alguien publica una imagen con un gráfico de dispersión y una línea de ajuste, y lanza alguna afirmación para interpretarlo: “Comer chocolate correlaciona con la calidad del sexo”, “Las personas con mejor gusto para vestir tienen más parejas”… El último caso que recuerdo (y lo selecciono porque afortunadamente no ha sido ni de lejos de los más polémicos) ocurrió cuando alguien posteó este aparentemente inocente gráfico con algunas correlaciones entre renta y voto.

Y se lía. Ya digo que en esta ocasión la gente estuvo muy civilizada e incluso dada al diálogo (chapeau, gente!), pero otras veces por poco se llega a las manos por una discusión casi idéntica, anda que si no está la pantalla en medio… Aun así, en todos estos flames podemos encontrar dos tipos de críticas recurrentes que son las que yo quería comentar:

1. “Oye, pero dónde vas, que esa nube de puntos no tiene “forma de línea”, y por tanto esos datos son aleatorios jajaja”.
2. “Sí, bueno, pero esa R cuadrado (tenéis el valor en el gráfico) es muy pequeña. Una R cuadrado de menos de 0.99 indica que no existe correlación, y por tanto esos datos son aleatorios. Es que los de las ciencias sociales no tenéis ni idea, jaja”.

Antes de pasar a analizar estos argumentos, que es lo que encuentro interesante, aprovecho para mencionar que me parecen muy reveladoras las formas y los modos de quienes suelen escribirlos, más que nada porque indican que por debajo hay toda una serie de creencias erróneas en torno a la ciencia, los datos, la probabilidad… Y viniendo de gente con perfiles en los que exhiben título de carrera técnica (y alusiones a las criptomonedas, habitualmente). Vaya tela. Os pongo alguna perla de ejemplo:

PERLA #1: “Si le entrego a mi jefe/profesor esa correlación tan baja, me despide”

Ah, perdona. Yo creía que la ciencia consiste justo en intentar comprender la realidad y para ello usamos las matemáticas y la estadística, para hacer estimaciones e interpretar los datos. No sabía que el objetivo es obtener modelos con ajustes perfectos independientemente de cuáles sean los fenómenos de estudio, y que la consecuencia de no conseguirlos iba a ser mi despido. Pues nada, falseo los datos, o bien overfitteo, y ya está: ajuste perfecto y a vivir engañado, que eres un crack, un titán, un mastodonte.

PERLA #2: “Yo ahí no distingo a ojo ninguna correlación, por lo tanto no hace falta estadística.

Claro, hombre. Y nosotros, los tontos, perdiendo el tiempo analizando los datos y obteniendo estimadores y calculando p-valores… Imagino que esta gente, para saber la hora, mirará la sombra de los edificios en vez de consultar un reloj, y calculará las distancias a ojo (“¿que a cuántos Km está el pueblo? Náh, a unas dos o tres escuchas de Bohemian Rhapsody yendo a velocidad normal, ni muy lento ni como si tuviera ganas de llegar, jajaja”).

Aquí el dibujante Randall Munroe, el de xkcd, también patinó lo suyo, y por eso aparece a menudo en esos flames turras apoyando este argumento:

En fin. Que a veces estas discusiones son todo un catálogo de prepotencia y Dunning-Kruger, y que mucha de esta gente, por sus respuestas, deduzco que no ha analizado en su vida datos que hayan salido del mundo real en campos como la psicología, la biología o la medicina. Porque si no, no se entiende este empeño en equivocarse y encima alardear de ello. Pero vamos a pasar por alto las formas y a centrarnos en los argumentos que esgrime esta gente, porque eso sí me interesa dejarlo claro. Te cuento.

“Nubes de puntos” y el problema de estimar correlaciones “a ojo”

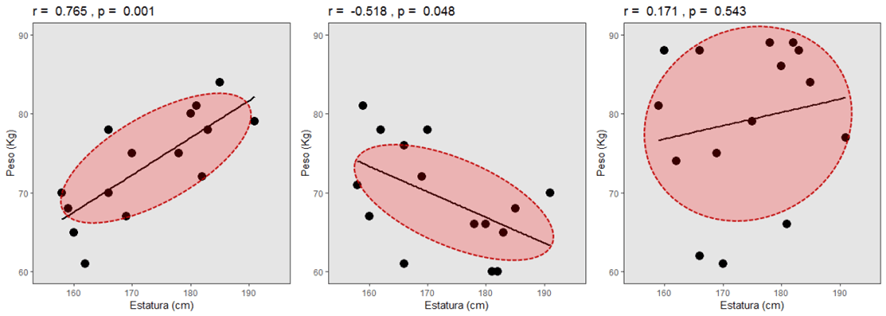
Esto ya te lo sabes, porque lo hemos contado en el blog anteriormente: en principio, la forma que adopta una nube de puntos te da una pista de la magnitud y dirección de una correlación:

Y por eso todo el mundo quiere ver los gráficos, y espera encontrar esas formas reconocibles.

Lo que pasa, querido amigo, es que, lamentándolo mucho, ni tus ojos ni tu sistema cognitivo son perfectos e infalibles. Pueden engañarte la luz, la escala, los colores. Pero ojo, también tus motivaciones e intereses, tus expectativas… Así que no, no podemos evaluar correlaciones a ojo. Y si quieres algo de ciencia que avale lo que digo, hay por ahí algún estudio de psicofísica sobre percepción de correlaciones a ojo, e indica que es una tarea que a los humanos se nos da realmente mal (Elliott, 2021).

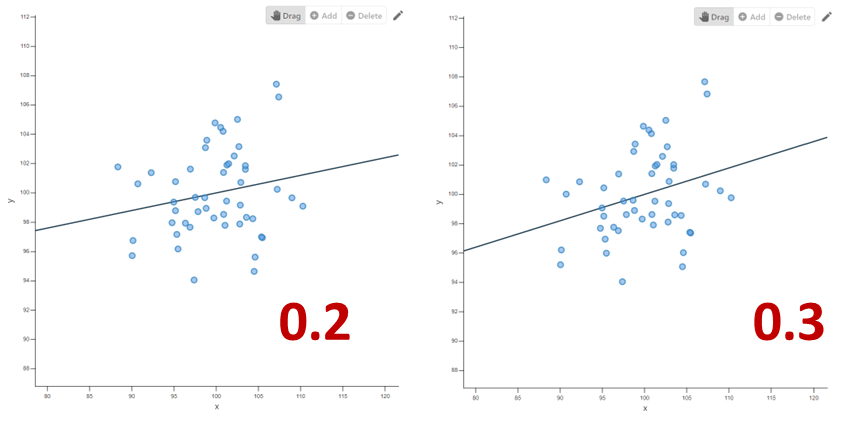
O, si quieres algo un poco más interactivo, prueba a comparar este par de nubes de puntos que he generado con este visualizador de correlaciones: ¿las distingues entre sí? Está difícil. A la izquierda, correlación de 0.20. A la derecha, correlación de 0.30. Ya puedes tener buen ojo para diferenciarlas.

Y luego está el hecho de que los datos reales pueden ser más ruidosos y feos que los de las simulaciones. En ocasiones la correlación está ahí aunque el aspecto de la nube engañe.

Voy a seguir el ejemplo de Richard McElreath. Prueba a ejecutar el siguiente código en R:

set.seed(123)
N <- 200
X <- rnorm(N)
Y <- rnorm(N, 0.4*X)

Ahora tenemos dos variables, X e Y. Aunque las hemos generado con una semilla aleatoria, ambas correlacionarán con un coeficiente de aproximadamente r = 0.4, que es un efecto bastante fuerte. Aun así puede que la nube de puntos no parezca muy sugerente:

plot(X, Y, col = 2, lwd = 2, xlim = c(-4, 4), ylim = c(-4, 4))
abline(lm(Y ~ X))

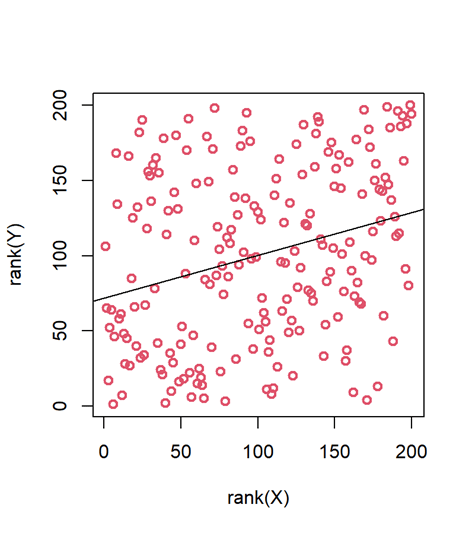
Y te lo voy a poner peor. Una transformación habitual en algunos escenarios es lo que llaman “rank transformation”, o transformación por rango: reemplazamos los valores por su posición ordenada en la muestra, en función de su magnitud. Esto se hace en algunas situaciones en las que, por lo que sea, optamos por métodos no paramétricos de inferencia. Pues bien, la nube de puntos tiene este aspecto cuando la transformamos así:

plot(rank(X), rank(Y), col = 2, lwd = 2)
abline(lm(rank(Y) ~ rank(X)))

¿Qué? ¿A que no tiene pinta de correlacionar? Ahí no hay forma de línea, la nube no apunta hacia arriba, parece todo muy aleatorio y ruidoso… Pero las dos variables correlacionan. Comprobémoslo:

cor.test(rank(X), rank(Y))

	Pearson's product-moment correlation

data:  rank(X) and rank(Y)
t = 4.1878, df = 198, p-value = 4.237e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.1525463 0.4078501
sample estimates:
      cor 
0.2852501 

Lo creas o no, ahí existe una correlación, y es significativa (p < 0.001). Tus ojos y tus expectativas te pueden engañar.

Piensa que, al fin y al cabo, inventamos la estadística justo para eso: para no dejarnos engañar por nuestros sesgos y limitaciones, y para ayudarnos a separar la señal del ruido, aunque este aparente significar algo más. Que justo calculamos coeficientes de correlación, estimadores, p-valores y todo eso por ese preciso motivo. Para que vengas tú ahora con tu ojo biónico a hacer estimaciones de brocha gorda en pleno 2023.

Recuerda: si quieres saber si en un set de datos hay señal (correlación) o simplemente ruido, una cosa que puedes hacer es calcular el p-valor, que te sacará de dudas. En este ejemplo concreto, el p valor es significativo, lo cual quiere decir que la correlación, visible o no a simple vista, es distinguible entre el ruido. 

“Lo siento, tu R cuadrado es muy pequeña”

Más allá de los que se empeñan en juzgar las correlaciones “a ojímetro”, tenemos la otra variante de comentario escéptico que os he dicho antes: esa gente que mira el grado de ajuste (a menudo medido con ese estadístico llamado R cuadrado) y dice que “bah, es muy pequeña, eso no demuestra que exista una relación, solo estás mirando ruido”. A menudo los dos comentarios van juntos, puesto que una nube de puntos bien compactada en torno a la línea de ajuste va a tener casi siempre un valor elevado de R cuadrado, mientras que un ajuste bajo se acompañará de una nube dispersa. Pero vamos a comentarlo…

¿Qué es la R cuadrado? El estadístico R cuadrado, conocido como “coeficiente de determinación” se utiliza a veces como una cuantificación del tamaño del efecto (en este caso, de la magnitud de la correlación entre dos variables). Os contaré qué significa, y luego vamos al tema que nos ocupa.

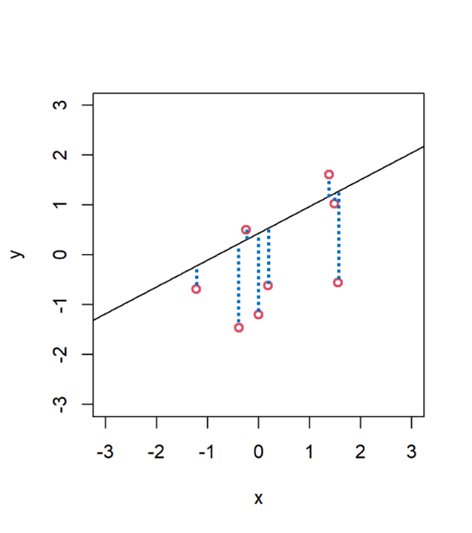
Cuando ajustamos una línea a una nube de puntos, observaremos que no todos los puntos caen exactamente en la línea, sino que se quedan flotando más o menos “alrededor”. Esto únicamente quiere decir que nuestro modelo (que se representa con la línea) no es perfecto. Que hay cierto error asociado a la predicción. Ese error de predicción que está cometiendo nuestro modelo lo podemos calcular al agregar todas las distancias entre cada punto y la predicción (la línea), lo que habitualmente se llaman “residuos” del modelo. Cuanto más lejos estén los puntos de la línea, más error y por lo tanto peor es mi modelo.

Pero para calcular la R cuadrado, también influye la variabilidad que hay en nuestros datos (cómo de separados están los datos de la media), un atributo que represento en esta otra figura. La línea horizontal es la media de la variable dependiente (y). Cuanto más dispersos están los puntos alrededor de esa línea, más variabilidad o “ruido”.

En realidad, la R cuadrado viene dada por el cociente entre esos dos grupos de distancias: la cantidad agregada de error de predicción que cometemos, y la variabilidad de los datos. Es decir, la R cuadrado es una proporción que expresa “cuánta señal” hay en tus datos con respecto a la cantidad de ruido aleatorio que contienen.

Así, una R cuadrado grande (cercana a 1) nos dice que nuestro modelo predice muy ajustadamente los datos (hay más señal que ruido). Una R cuadrado pequeñita (cercana a 0) nos diría que nuestro modelo no predice bien los datos, “no ajusta bien”, porque no produce distancias residuales mucho menores que el más simple de los modelos: la media de y. De hecho, se puede expresar la R cuadrado como el porcentaje de varianza “explicada” o “capturada” por el modelo.

O sea, que en la imagen de la izquierda, x predice el 98% de la variabilidad en y, pero en la imagen de la derecha solo predice un 6%. Al simular los datos para hacer las figuras, lo único que he cambiado entre ambas es la cantidad de variabilidad aleatoria (“ruido”) en la variable dependiente, pero la correlación real (poblacional) entre las variables es idéntica.

Vale, entonces: ¿qué pasa si mi R cuadrado es baja? Pues esto nos indica que tu modelo no captura una parte sustancial de la variabilidad en y. Esto puede significar que tal vez no has incluido en el modelo alguna variable predictora relevante (de ahí el error grande en el numerador de la ecuación), o que tus medidas no son buenas y hay muchísimo ruido (de ahí un valor grande en el denominador)… O simplemente que la asociación que buscas entre x e y es pequeña. Es decir, y por resumir: que la variable y (como el voto en la gráfica de arriba) depende de muchas cosas, entre ellas x, pero no solo x.

Pero, aquí va lo importante: ¿me está diciendo este estadístico si mis datos “son aleatorios”? No, solo me está indicando que mi modelo es insuficiente para explicar el 100% de la variabilidad en la variable dependiente. El modelo explica una parte más o menos pequeña de esa variabilidad. O sea, la asociación entre las dos variables presenta un efecto pequeño.  

Que un efecto sea pequeño no quiere decir que sea inexistente. O que no sea consistente. O que no sea relevante. Solo es eso, pequeño. El caso es que, en Twitter y en otros lugares, no faltará quien señale una R cuadrado de menos de 0.70 y grite: “¡Esa correlación no existe porque la R cuadrado no es de 0.99!”.

El problema de los efectos pequeños

(Si lo necesitas, repasa este post sobre el tamaño del efecto).

Reflexionemos un poco sobre los efectos pequeños. Para empezar, podemos plantearnos a qué porras le llamamos “efecto pequeño”. Y es que no es ninguna tontería la pregunta. ¿Dónde ponemos la frontera entre un efecto pequeño, uno mediano y uno grande?

Existen algunas indicaciones, pero no dejan de ser convenciones un tanto arbitrarias. Por ejemplo, Cohen considera que una correlación menor de r = 0.3 se considera “pequeña”, y una de más de r = 0.5 se considera “grande”. Pero claro, esto es meramente una guía para hacerse una idea y no nos dice mucho sin saber el contexto (¿es un estudio de psicología? ¿de ingeniería? ¿es un experimento de laboratorio o una medición al natural?). Yo no os animo a hablar de efectos “grandes” o “pequeños” así en el vacío, sin un contexto.

Aun así, hay algunos comentarios en Twitter que parecen asumir que una R cuadrado menor de 0.8 es “basura” (literalmente lo han dicho). A lo mejor aquí alguno de esos comentaristas se lleva una sorpresa: ¡La R cuadrado en realidad es *menor* de lo que creen! En modelos sencillos como la mayoría de los gráficos de puntos que se comparten en redes, solo tenemos una pareja de variables, x e y. En la mayoría de esos casos, el ajuste (R cuadrado) del modelo coincide con el cuadrado del coeficiente de correlación de Pearson, r. O sea, que si tomamos lo que para Cohen es una correlación grande de r = 0.8, vemos que corresponde a una R cuadrado de 0.8^2 = 0.64, que no suena tan “potente”. Así que cuando los tuiteros con carreras técnicas critican una R cuadrado de 0.25 por ser despreciable, que sepáis que realmente corresponde a un efecto de tamaño mediano-grande para una correlación (r = 0.50) según las convenciones como la de Cohen, y lo que probablemente ocurre es que esta gente no sabe lo que significa R cuadrado. En fin.

Si queréis hacer conversiones entre distintos estadísticos estandarizados para el tamaño del efecto, podéis acudir a esta web. Podréis, por ejemplo, pasar de R cuadrado a d de Cohen, o a r de Pearson… Lo que queráis. Eso sí, con algunas cautelas porque las traducciones no son siempre perfectas y dependen de más cosas que no estamos comentando. Pero si jugáis un poco, veréis cómo a veces las equivalencias no son las que la gente asume en internet. Por ejemplo, si os ayuda a visualizarlo mejor, una R cuadrado de 0.20 corresponde a una correlación de Pearson de r = 0.45, ¡y una d de Cohen de 1!

Pero quizá ayude un poco más ver las cosas en su contexto. Os doy algunas pistas:

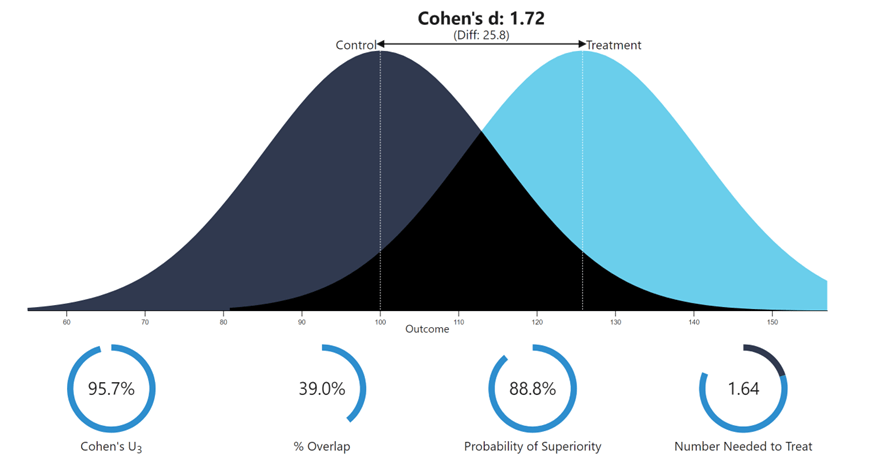
• La diferencia de estatura promedio entre hombres y mujeres es lo bastante grande como para verla “a simple vista”. Quiero decir, seguramente nadie necesite mirar una estadística y calcular un p-valor para averiguar que la diferencia existe, y que por lo general los hombres suelen ser, en promedio, más altos que las mujeres, ¿verdad? Pues bueno, esa diferencia tiene un tamaño de d = 1.72. O lo que es lo mismo, una r = 0.65, o una R cuadrado de 0.42. Un efecto que podemos considerar, seguramente, grande. Lo veis aquí:

Aun así, podéis ver cómo hay un porcentaje de hombres más bajos que muchas mujeres, y que hay solapamiento entre las distribuciones, como es lógico. ¡Y sigue siendo un efecto grande aunque la R cuadrado sea de menos 0.50!

• Otra situación en la que esperaríamos efectos grandes es cuando correlacionamos una variable consigo misma. Que me diréis: ¿esto para qué querría hacerlo? Pues bien, en psicometría esto se hace de manera recurrente al validar cuestionarios. Generalmente, se obtienen medidas de la correlación de un cuestionario en ocasiones sucesivas en el mismo individuo, o se dividen los ítems en dos mitades para ver cómo correlacionan entre sí… En estos casos, esperaríamos correlaciones altas, ya que estamos correlacionando algo “consigo mismo”, ¿verdad? Pues bueno. Los psicómetras consideran aceptables los valores de r mayores de 0.70 (R cuadrado de 0.49). ¡Y estamos hablando de algo correlacionando consigo mismo! ¿En qué situación cabría esperar correlaciones mayores?
• Seguro que habéis usado alguna vez un analgésico como el ibuprofeno. Creo que hay consenso en que este tipo de medicamentos funciona para calmar el dolor, ¿verdad? Pues algunas estimaciones del tamaño del efecto analgésico nos dicen que ronda el valor de r = 0.14 (R cuadrado 0.02). Otras, un poco mayor, r = 0.21 (R cuadrado 0.04). Uno de los comentaristas criptobros de Twitter no tardaría en deciros que es “puro ruido”. 🤦‍♂️

De todo esto podemos concluir ciertas cosas sobre los efectos pequeños, algunas de ellas no tan evidentes como mucha gente cree. Lo primero es que los efectos pequeños no tienen por qué ser insignificantes. De hecho pueden ser importantes. Pensad en el ibuprofeno. El efecto es estadísticamente pequeño, pero lo suficientemente sólido como para que millones de personas lo utilicen. O, mejor aún: imaginad un tratamiento para una enfermedad mortal que solo cura al 5% de quienes la toman. Es una tasa de éxito mínima, pero si no hay otro tratamiento disponible ¡yo tengo claro que lo tomaría!

A veces los efectos pequeños se vuelven más importantes por efecto acumulativo. Tomar el sol durante 10 minutos seguidos implica una exposición mínima a la radiación ionizante, y seguramente nadie te diría que eso va a incrementar sustancialmente la probabilidad de desarrollar un melanoma. Ahora bien, si la exposición es más prolongada y repetida, ese efecto minúsculo, pero acumulado, puede acabar en un cáncer de piel, ¿verdad?

Otras veces la importancia práctica de un efecto no viene tan determinada por su tamaño, sino más bien por otros factores como su consistencia. La historia de la ciencia contiene ejemplos de efectos minúsculos pero regulares que han llevado a descubrimientos fundamentales sobre las leyes de la materia. Por si te ayuda a visualizarlo: imagina una relación entre dos variables que es muy débil, pero contiene muy poco ruido.

En cualquier caso, nunca deberías cometer el error de interpretar un tamaño del efecto en el vacío. Influirán muchas cosas como por ejemplo el campo de estudio, la situación en la que se recogen los datos… A pesar de lo que dice el ejército de cuñaos:

…Porque sí, necesitas un contexto para interpretar el tamaño del efecto: ¿A qué llamamos efecto “grande” o “pequeño”? Una pastilla que funciona en el 20% de la gente para aliviar algún problema podría ser lo bastante buena. Un avión que se estrellara solo el 0.01% del tiempo sería inaceptable.

Un matiz que puede ser relevante: ¿qué tipo de fenómeno estamos describendo? Un efecto observado en laboratorio, en situaciones controladas, será probablemente más grande que uno observado en el mundo real, en un trabajo de campo sin tanto control. Sospecho que la sorpresa de algunos comentaristas desubicados con carrera técnica viene de aquí: en campos que tratan con datos “reales” (biología, medicina…) es común que los efectos sean más pequeños porque los fenómenos son complejos y multicausales, y los efectos que se ven en el laboratorio quedan más diluidos en el ruido cuando se miden en el mundo real. En ciencias sociales, esto es todavía más claro. En psicología, salvo que hablemos de un efecto observado en un experimento de laboratorio, encontrar correlaciones de r = 0.3 o mayores en un estudio de campo nos parece suficiente. Y si esos efectos son consistentes y se replican… Qué más quieres.

Conclusiones

Para ir cerrando, vamos a recopilar lo que (se supone) hemos aprendido hoy:

• Tus sentidos y tu sistema cognitivo te pueden jugar una mala pasada. Necesitas la estadística justo para compensar esos sesgos y limitaciones. No seas cafre y no juzgues los datos “a ojo”.
• El que un efecto sea pequeño no quiere decir que sea inexistente. Son cosas distintas, la estimación del tamaño del efecto observado y la capacidad de distinguirlo entre el ruido. Para lo segundo se inventó la estadística inferencial.
• El que un efecto sea pequeño no implica que sea insignificante o despreciable. Hay ejemplos de efectos de magnitud pequeña o mediana, pero muy relevantes en la práctica.

Bonus: Lo que sí podrías criticar

Claro, si estás en Twitter será porque te va la marcha, y no puedes dejar pasar la oportunidad de criticar y destrozar a todo el que tú creas que se equivoca, ¿verdad? Pues venga, que no se diga: te voy a ayudar dándote unos cuantos argumentos de crítica que sí tendrían sentido. Así, cuando te pongan delante una figura de puntos y la quieras desacreditar, piensa…

• ¿De dónde salen los datos? ¿Es una fuente fiable?
• ¿Tiene sentido teórico o lógico la relación que se está planteando?
• ¿De verdad estás buscando una relación lineal? (Porque a veces se ven datos que piden a gritos un ajuste cuadrático, por ejemplo)
• ¿Cómo se ha seleccionado la muestra? ¿Podría no ser representativa, o ser un ejemplo de cherry-picking…?
• ¿Es una muestra lo bastante grande? (y ojo, que para esto tampoco valen los juicios “a ojímetro”, ya que el tamaño será apropiado o no en función de muchos condicionantes)
• ¿Se cumplen los supuestos del análisis?
• ¿No estarán interpretando una correlación en términos causales? Ya sabes que eso no se hace, salvo que tengas muy, muy, claro lo que estás haciendo y lo mucho que puedes meter la pata.